DL notes 01:RNN/LSTM/GRU
@[toc]
一、RNN基本结构、梯度消失和梯度爆炸的原因
线性计算单元组成的RNN结构是最简单的一种,我们以此为例来说明造成梯度消失和梯度爆炸的原因:
 上图为线性计算单元组成的RNN.依据上图,我们现假设存在一个RNN模型仅包含一个隐藏层,整个RNN模型关注的时间步数为3,$H{0}$H{1} = W{X}X{1} + W{H}H{0} + b{H}, O{1} = W{O}H{1} + b{O} H{2} = W{X}X{2} + W{H}H{1} + b{H}, O{2} = W{O}H{2} + b{O} H{3} = W{X}X{3} + W{H}H{2} + b{H}, O{3} = W{O}H{3} + b{O} $$
上图为线性计算单元组成的RNN.依据上图,我们现假设存在一个RNN模型仅包含一个隐藏层,整个RNN模型关注的时间步数为3,$H{0}$H{1} = W{X}X{1} + W{H}H{0} + b{H}, O{1} = W{O}H{1} + b{O} H{2} = W{X}X{2} + W{H}H{1} + b{H}, O{2} = W{O}H{2} + b{O} H{3} = W{X}X{3} + W{H}H{2} + b{H}, O{3} = W{O}H{3} + b{O} $$
其中$X =[X{0},X{1},X{2},..X{t}]Y =[Y{0},Y{1},Y{2},..Y{t}]tH =[H{0},H{1},H{2},..H{t}]W{X},W{H},W{O}b{H},b{O}$L{t} = \frac{1}{2}\left(Y{t}-O{t}\right)^{2} L = \sum{t=0}^{T} L{t}$$ 假设目前只考虑初始的三个时间步长,我们选取最长一条反向传播通路为例,即以$L{3}$ \frac{\partial L{3}}{\partial W{O}} = \frac{\partial L{3}}{\partial O{3}} \frac{\partial O{3}}{\partial W{O}} $$
$$ \frac{\partial L{3}}{\partial W{X}} = \frac{\partial L{3}}{\partial O{3}} \frac{\partial O{3}}{\partial H{3}} \frac{\partial H{3}}{\partial W{X}} + \frac{\partial L{3}}{\partial O{3}} \frac{\partial O{3}}{\partial H{3}} \frac{\partial H{3}}{\partial H{2}} \frac{\partial H{2}}{\partial W{X}} + \frac{\partial L{3}}{\partial O{3}} \frac{\partial O{3}}{\partial H{3}} \frac{\partial H{3}}{\partial H{2}} \frac{\partial H{2}}{\partial H{1}} \frac{\partial H{1}}{\partial W{X}}$$
$$ \frac{\partial L{3}}{\partial W{H}} = \frac{\partial L{3}}{\partial O{3}} \frac{\partial O{3}}{\partial H{3}} \frac{\partial H{3}}{\partial W{H}} + \frac{\partial L{3}}{\partial O{3}} \frac{\partial O{3}}{\partial H{3}} \frac{\partial H{3}}{\partial H{2}} \frac{\partial H{2}}{\partial W{H}} + \frac{\partial L{3}}{\partial O{3}} \frac{\partial O{3}}{\partial H{3}} \frac{\partial H{3}}{\partial H{2}} \frac{\partial H{2}}{\partial H{1}} \frac{\partial H{1}}{\partial W{H}}$$
从中可以发现根据链式法则求导,$W{X},W{H}W{X},W{H}HtW{X}$ \frac{\partial L{t}}{\partial W{X}} = \sum{k=0}^{t} \frac{\partial L{t}}{\partial O{t}} \frac{\partial O{t}}{\partial H{t}} \left( \prod{j=k+1}^{t} \frac{\partial H{j}}{\partial H{j-1}} \right) \frac{\partial H{k}}{\partial W{X}} $$ 任意时刻损失函数对$W{H}W{X}tanh$H{j} = tanh(W{X}X{j}+W{H}H{j-1}+b{H})\prod{j=k+1}^{t} \frac{\partial H{j}}{\partial H{j-1}} = \prod{j=k+1}^{t} tanh^{‘}·W{H}tanh^{‘} x= 1-tanh^{2}x$$ 因此可知。 在训练过程中,$H{j}tanh^{‘}W{H}(0,1)\prod{j=k+1}^{t} tanh^{‘}·W{H}W{H}\prod{j=k+1}^{t} tanh^{‘}·W{H}$ 连乘后结果趋近于无穷,导致梯度爆炸。 如何避免这种现象?在RNN的课程学习中,提到裁剪梯度的方法,假设我们把所有模型参数的梯度拼接成一个向量 ,并设裁剪的阈值是 。裁剪后的梯度即: 梯度的的 $L{2}\theta$。函数如下:
def grad_clipping(params, theta, device):
norm = torch.tensor([0.0], device=device)
for param in params:
norm += (param.grad.data ** 2).sum()
norm = norm.sqrt().item()
if norm > theta:
for param in params:
param.grad.data *= (theta / norm)裁剪梯度是一个简单好用的防止梯度爆炸的方法,实际上造成梯度衰减或梯度爆炸的根本原因是$\prod{j=k+1}^{t} \frac{\partial H{j}}{\partial H{j-1}}\frac{\partial H{j}}{\partial H_{j-1}} \in [0,1]$其实这就是LSTM做的事情,至于细节如何则会在后续的篇幅中加以介绍。
二、LSTM
长短期记忆(Long short-term memory, LSTM)是一种特殊的RNN结构单元,主要是为了解决长序列训练过程中的梯度消失和梯度爆炸问题。简单来说,就是相比普通的RNN,LSTM能够在更长的序列中有更好的表现。
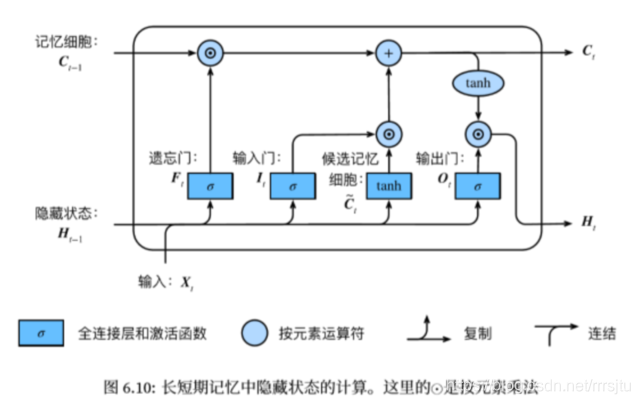 $$I_t = σ(XtW{xi} + H{t−1}W{hi} + b_i) F_t = σ(XtW{xf} + H{t−1}W{hf} + b_f) O_t = σ(XtW{xo} + H{t−1}W{ho} + b_o) \widetilde{C}_t = tanh(XtW{xc} + H{t−1}W{hc} + b_c) C_t = Ft ⊙C{t−1} + I_t ⊙\widetilde{C}_t H_t = O_t⊙tanh(Ct)Y{t} = \phi(H{t}W{hy}+b{y})$$
相比RNN只有一个传递状态$H{t}C{t}H{t}C{t}C{t}C{t-1}H{t}\odot\oplus$ 则代表进行矩阵加法。
$$I_t = σ(XtW{xi} + H{t−1}W{hi} + b_i) F_t = σ(XtW{xf} + H{t−1}W{hf} + b_f) O_t = σ(XtW{xo} + H{t−1}W{ho} + b_o) \widetilde{C}_t = tanh(XtW{xc} + H{t−1}W{hc} + b_c) C_t = Ft ⊙C{t−1} + I_t ⊙\widetilde{C}_t H_t = O_t⊙tanh(Ct)Y{t} = \phi(H{t}W{hy}+b{y})$$
相比RNN只有一个传递状态$H{t}C{t}H{t}C{t}C{t}C{t-1}H{t}\odot\oplus$ 则代表进行矩阵加法。
LSTM主要包括以下几个结构: - 遗忘门:控制上一时间步的记忆细胞 - 输入门:控制当前时间步的输入 - 输出门:控制从记忆细胞到隐藏状态 - 记忆细胞:⼀种特殊的隐藏状态的信息的流动 三个门输出都经过诸如的激活函数,映射到的范围,形成门控状态。而记忆细胞则是通过转换成的范围,这里作为记忆细胞短期依赖输出而非门控信号。
LSTM 内部主要有三个阶段:
忘记阶段。这个阶段主要是对上一个节点传进来的输入进行选择性忘记。简单来说就是会 “忘记不重要的,记住重要的”。具体来说是通过计算得到的 $F{t}C{t-1}$ 哪些需要留哪些需要忘。
选择记忆阶段。这个阶段将这个阶段的输入有选择性地进行“记忆”。主要是会对输入 进行选择记忆。哪些重要则着重记录下来,哪些不重要,则少记一些。当前的输入内容由前面计算得到的$\widetilde{C}tI{t}C_{t}tanh$起到对输入的信息进行压缩的作用。
输出阶段。这个阶段将决定哪些将会被当成当前状态的输出。主要是通过 $O{t}C{t}$进行了放缩(通过一个tanh激活函数进行变化)。
与普通RNN类似,输出 $Y{t}H{t}$变化得到。
三、GRU
GRU(Gate Recurrent Unit)是循环神经网络(Recurrent Neural Network, RNN)的一种。和LSTM(Long-Short Term Memory)一样,也是为了解决长期记忆和反向传播中的梯度等问题而提出来的。
GRU和LSTM在很多情况下实际表现上相差无几,那么为什么我们要使用新人GRU(2014年提出)而不是相对经受了更多考验的LSTM(1997提出)呢?其实通过代码我们就可以发现,GRU的权重参数相比LSTM减少了1/4。相比LSTM,使用GRU能够达到相当的效果,并且相比之下更容易进行训练,能够很大程度上提高训练效率,因此很多时候会更倾向于使用GRU。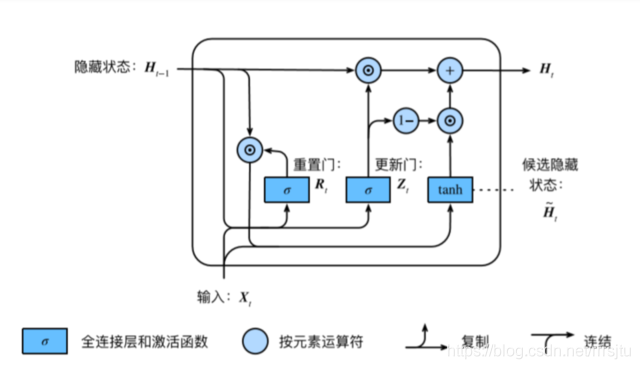 $$R_{t} = σ(XtW{xr} + H{t−1}W{hr} + br) Z{t} = σ(XtW{xz} + H{t−1}W{hz} + bz) \widetilde{H}{t-1} = Rt ⊙H{t−1} \widetilde{H}_t = tanh(XtW{xh} + \widetilde{H}{t-1}W{hh} + b_h) H_t = Zt⊙H{t−1} + (1−Z_t)⊙\widetilde{H}_t $$
$$R_{t} = σ(XtW{xr} + H{t−1}W{hr} + br) Z{t} = σ(XtW{xz} + H{t−1}W{hz} + bz) \widetilde{H}{t-1} = Rt ⊙H{t−1} \widetilde{H}_t = tanh(XtW{xh} + \widetilde{H}{t-1}W{hh} + b_h) H_t = Zt⊙H{t−1} + (1−Z_t)⊙\widetilde{H}_t $$
GRU很聪明的一点就在于,我们使用了同一个门控 就同时可以进行遗忘和选择记忆(LSTM则要使用多个门控)。在GRU中被称作重置⻔有助于捕捉时间序列⾥短期的依赖关系;被称作更新⻔有助于捕捉时间序列⾥⻓期的依赖关系。 $Zt⊙H{t−1}ZtH{t−1}(1−Z_t)⊙\widetilde{H}_t\widetilde{H}_t(1−Z_t)\widetilde{H}_t\widetilde{H}_tH_t = Zt⊙H{t−1} + (1−Z_t)⊙\widetilde{H}tH{t−1}Z_t(1−Z_t)Z_t\widetilde{H}_t(1−Z_t)$。以保持一种”恒定“状态。
四、深度循环神经网络
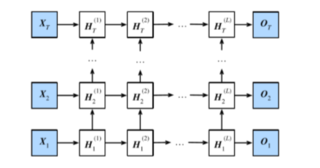 $$\boldsymbol{H}_t^{(1)} = \phi(\boldsymbol{X}t \boldsymbol{W}{xh}^{(1)} + \boldsymbol{H}{t-1}^{(1)} \boldsymbol{W}{hh}^{(1)} + \boldsymbol{b}_h^{(1)})
\boldsymbol{H}_t^{(\ell)} = \phi(\boldsymbol{H}t^{(\ell-1)} \boldsymbol{W}{xh}^{(\ell)} + \boldsymbol{H}{t-1}^{(\ell)} \boldsymbol{W}{hh}^{(\ell)} + \boldsymbol{b}_h^{(\ell)})\boldsymbol{O}_t = \boldsymbol{H}t^{(L)} \boldsymbol{W}{hq} + \boldsymbol{b}_q$$
在pytorch的实现中以
$$\boldsymbol{H}_t^{(1)} = \phi(\boldsymbol{X}t \boldsymbol{W}{xh}^{(1)} + \boldsymbol{H}{t-1}^{(1)} \boldsymbol{W}{hh}^{(1)} + \boldsymbol{b}_h^{(1)})
\boldsymbol{H}_t^{(\ell)} = \phi(\boldsymbol{H}t^{(\ell-1)} \boldsymbol{W}{xh}^{(\ell)} + \boldsymbol{H}{t-1}^{(\ell)} \boldsymbol{W}{hh}^{(\ell)} + \boldsymbol{b}_h^{(\ell)})\boldsymbol{O}_t = \boldsymbol{H}t^{(L)} \boldsymbol{W}{hq} + \boldsymbol{b}_q$$
在pytorch的实现中以num_layers参数进行层数的设置和调整。
五、双向循环神经网络
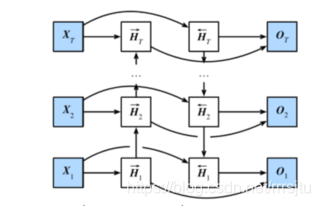 $$\overrightarrow{\boldsymbol{H}}_t = \phi(\boldsymbol{X}t \boldsymbol{W}{xh}^{(f)} + \overrightarrow{\boldsymbol{H}}{t-1} \boldsymbol{W}{hh}^{(f)} + \boldsymbol{b}_h^{(f)}) \overleftarrow{\boldsymbol{H}}_t = \phi(\boldsymbol{X}t \boldsymbol{W}{xh}^{(b)} + \overleftarrow{\boldsymbol{H}}{t+1} \boldsymbol{W}{hh}^{(b)} + \boldsymbol{b}_h^{(b)}) \boldsymbol{H}t=(\overrightarrow{\boldsymbol{H}}{t}, \overleftarrow{\boldsymbol{H}}_t)\boldsymbol{O}_t = \boldsymbol{H}t \boldsymbol{W}{hq} + \boldsymbol{b}_q$$
在pytorch的实现中以
$$\overrightarrow{\boldsymbol{H}}_t = \phi(\boldsymbol{X}t \boldsymbol{W}{xh}^{(f)} + \overrightarrow{\boldsymbol{H}}{t-1} \boldsymbol{W}{hh}^{(f)} + \boldsymbol{b}_h^{(f)}) \overleftarrow{\boldsymbol{H}}_t = \phi(\boldsymbol{X}t \boldsymbol{W}{xh}^{(b)} + \overleftarrow{\boldsymbol{H}}{t+1} \boldsymbol{W}{hh}^{(b)} + \boldsymbol{b}_h^{(b)}) \boldsymbol{H}t=(\overrightarrow{\boldsymbol{H}}{t}, \overleftarrow{\boldsymbol{H}}_t)\boldsymbol{O}_t = \boldsymbol{H}t \boldsymbol{W}{hq} + \boldsymbol{b}_q$$
在pytorch的实现中以bidirectional参数进行层数的设置和调整。